bloque 4

*RECONOCE LAS PROPIEDADES DE LOS POLIGONOS*

En geometria, un polígono es una figura plana compuesta por una secuencia finita de segmentos rectos consecutivos que cierran una región en el espacio. Estos segmentos son llamados lados, y los puntos en que se intersectan se llaman vértices. El interior del polígono es llamado a veces su cuerpo. El polígono es el caso bidimensional del politopo, figura geométrica general definida para cualquier número de dimensiones. A su vez, un politopo de tres dimensiones se denomina poliedro, y de cuatro dimensiones se llama policoro.

Clasificación

Clasificación de polígonos según el número de lados
Nombre	nº lados
trígono, triángulo	3
tetrágono, cuadrángulo, cuadrilátero	4
pentágono	5
hexágono	6
heptágono	7
octógono u octágono	8
eneágono o nonágono	9
decágono	10
endecágono o undecágono	11
dodecágono	12
tridecágono	13
tetradecágono	14
pentadecágono	15
hexadecágono	16
heptadecágono	17
octodecágono	18
eneadecágono	19
isodecágono, icoságono	20
triacontágono	30
tetracontágono	40
pentacontágono	50
hexacontágono	60
heptacontágono	70
octocontágono	80
eneacontágono	90
hectágono	100
chiliágono	1000
miriágono	10 000
decemiriágono	100 000
hectamiriágono, megágono	1 000 000
apeirógono	∞

Los polígonos se clasifican por el número de sus lados según la tabla adjunta, o bien por la forma de su contorno.

Polígono Simple Convexo Regular Irregular Cóncavo Complejo

Un polígono, por la forma de su contorno, se denomina

• Simple, si ningún par de aristas no consecutivas se corta.
• Complejo, si dos de sus aristas no consecutivas se intersecan.
• Convexo, si al atravesarlo una recta lo corta en un máximo de dos puntos, es el que tiene todos sus ángulos menores que 180º.
• Cóncavo, si al atravesarlo una recta puede cortarlo en más de dos puntos; es el que tiene uno o varios ángulos mayores que 180º.
• Equilátero, si tiene todos sus lados iguales.
• Equiángulo, si tiene todos sus ángulos iguales.
• Regular, si es equilátero y equiángulo a la vez.
• Irregular, si tiene sus ángulos y lados desiguales.
• Ortogonal o isotético, si todos sus lados son paralelos a los ejes cartesianos o .⁶
• Alabeado, si sus lados no están en el mismo plano.
• Estrellado, si se construye a partir de trazar diagonales en polígonos regulares. Se obtienen diferentes construcciones dependiendo de la unión de los vértices: de dos en dos, de tres en tres, etc.

• 

  Polígono simple, cóncavo e irregular.
  
• 

  Polígono complejo, cóncavo e irregular.
  
• 

  Polígono convexo y regular (equilátero y equiángulo).
  
• 

  Polígono estrellado.
  

 ELEMENTOS Y PROPIEDADES:


ANGULO CENTRAL;

Angulo central de un polígono regular

Es el formado por dos radios consecutivos.

Si n es el número de lados de un polígono:

Ángulo central = 360° : n

Ángulo central del pentágono regular= 360° : 5 = 72º

ANGULO INTERIOR;

Ángulos interiores de polígonos

Un ángulo interior es un ángulo dentro de una figura.

 

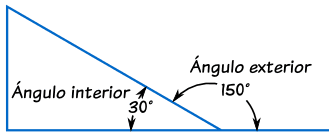
Ángulos exteriores de polígonos

Un ángulo exterior es un ángulo entre un lado de una figura y la línea que se extiende desde el lado siguiente.

LA SUMA DE LOS ANGULOS CENTRALES,INTERIORES Y EXTERIORES.

Conocemos la suma de los ángulos interiores de cualquier triángulo, que es 180º. Como cualquier polígono se puede dividir en triángulos se podrá calcular cuál es la suma total en cada caso. 

Un cuadrilátero se puede dividir en 2 triángulos, un pentágono en 3, un hexágono en 4, etc.; siempre dos menos que el número de lados. En definitiva, un polígono de n lados se puede descomponer en n-2 triángulos y, por tanto, la suma de los ángulos interiores será: 180º·(n-2). Si el polígono es regular el valor de uno de los ángulos interiores es: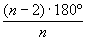

La suma de los ángulos exteriores de cualquier polígono es 360º. Teniendo en cuenta que el ángulo interior y el exterior suman 180º, en un polígono de n lados los interiores y los exteriores sumaran, en total, n·180º, como los interiores suman 180º·(n-2) los exteriores suman 360º

Nota: si sumas los ángulos interiores y exteriores sale el ángulo de una línea recta, 180°. 

PERIMETRO Y AREA DE LOS POLIGONOS REGULARES E IRREGULARES.

POLIGONO REGULAR :

Calcular el área de un polígono regular es una tarea bastante sencilla porque hay una fórmula que sirve para todos los polígonos regulares.

Encontrar el área de un polígono irregular es como jugar un juego en el que tienes que construir una forma con un montón de formas más pequeñas, hay que crear formas estándar y sumar las áreas de las formas para encontrar el área del polígono irregular. Sin embargo, ser capaz de hacer esto es más útil que saber cómo jugar a un juego. Peritos, agricultores y jardineros deben ser capaces de encontrar el área de piezas de forma irregular para trabajar con la tierra adecuadamente.


ejemplo:


 

Observa en la figura como se divide el hexágono regular en seis triángulos congruentes (misma forma y tamaño). Por lo tanto, el área del hexágono es igual a seis veces el área de cada triángulo.
Decimos: Área del hexágono = 6 x área del triángulo.
Ahora bien:

• La base de cada triángulo es un lado del hexágono.
• La altura de cada triángulo es la apotema del hexágono. Por lo tanto:

Área del triángulo = base x altura / 2 = lado x apotema / 2 y el área del hexágono = 6 x lado x apotema / 2
¡Pero 6 x lado es el perímetro del hexágono! Por lo tanto:
Área del hexágono = perímetro x apotema / 2
Esta formula es valida para todos los polígonos regulares:
Área del polígono = perímetro x apotema / 2

El área de un polígono regular es igual a la mitad del producto del perímetro por la apotema.

 POLIGONO IRREGULAR :

El área de un polígono irregular se puede hallar descomponiendo el polígono en otras figuras: triángulos, rectángulos, trapecios, etc.
Observa la figura. Se calcula el área de un polígono como suma de 3 triángulos y un trapecio:

• del triángulo ABE = 6 cm x 3 cm / 2 = 9 cm²
• del triángulo EDM = 2 cm x 3 cm / 2 = 3 cm²
• del trapecio MDCN = 3 cm + 2 cm / 2 x 3 cm = 7,5 cm²
• del triángulo NCB = 1 cm x 2 cm / 2 = 1 cm²

Área del polígono = 9 + 3 + 7,5 + 1 = 20,5 cm²