RESUELVE PROBLEMAS DE SEMEJANZA DE TRIANGULOS Y TEOREMA DE PITAGORAS.
En general, dos triángulos son semejantes
si tienen los ángulos homólogos iguales y sus lados proporcionales.
Se llaman Criterios de Semejanza de
dos triángulos, a un conjunto de condiciones tales que, si se cumplen,
tendremos la seguridad de que los triángulos son semejantes. Esos
criterios o casos son:

TEOREMA DE TALES
Existen dos teoremas en relación a la geometria clasica que reciben el nombre de teorema de Tales, ambos atribuidos al matemático griego Tales De Mileto en el siglo VI a. C.
Los dos teoremas de Tales
El primero de ellos explica esencialmente una forma de construir un triangulo semejante a uno previamente existente ("los triángulos semejantes son los que tienen iguales ángulos y sus lados homólogos proporcionales"). Mientras que el segundo desentraña una propiedad esencial de los circuncentros de todos los triángulos rectángulos ("encontrándose éstos en el punto medio de su hipotenusa"), que a su vez en la construcción geométrica es ampliamente utilizado para imponer condiciones de construcción de ángulos rectos. Si tres o más rectas paralelas son intersecadas cada una por dos transversales, los segmentos de las transversales determinados por las paralelas, son proporcionales.
Primer teorema
Como definición previa al enunciado del teorema, es necesario establecer que dos triángulos son semejantes si tienen los ángulos correspondientes iguales y sus lados son proporcionales entre sí. El primer teorema de Tales recoge uno de los resultados más básicos de la geometría, al saber, que:
Si en un triángulo se traza una línea paralela a cualquiera de sus lados, se obtiene un triángulo que es semejante al triángulo dado.
Segundo teorema
El segundo teorema de Tales de Mileto es un teorema de geometria particularmente enfocado a los triangulos,rectangulos, las circunferencias y los angulos inscritos, consiste en el siguiente enunciado:
Teorema segundo |
Demostración
-
- OA , OB y OC
Por lo tanto los triángulos AOB y BOC son isósceles.
La suma de los ángulos del triángulo ABC es:
Una aplicación del teorema de Tales se utiliza para dividir un segmento en varias partes iguales (con ayuda de compás, regla y escuadra o cartabón).
Ejemplo
Dividir el segmento AB en 3 partes iguales

TEOREMA DE PITAGORAS.
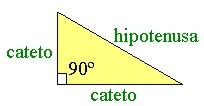
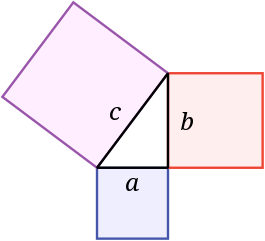
Teorema de Pitágoras
En todo triangulo rectangulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.
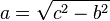 |
 |
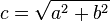 |
PROBLEMAS
1 La hipotenusa de un triángulo rectángulo mide 405.6 m y la proyección de un cateto sobre ella 60 m. Calcular:
1 Los catetos.
2 La altura relativa a la hipotenusa.
3 El área del triángulo.
2 Calcular los lados de un triángulo rectángulo sabiendo que la proyección de uno de los catetos sobre la hipotenusa es 6 cm y la altura relativa de la misma
3 Una escalera de 10 m de longitud está apoyada sobre la pared. El pie de la escalera dista 6 m de la pared. ¿Qué altura alcanza la escalera sobre la pared?
4 Determinar el lado de un triángulo equilátero cuyo perímetro es igual al de un cuadrado de 12 cm de lado. ¿Serán iguales sus áreas?
5Calcular el área de un triángulo equilátero inscrito en una circunferencia de radio 6 cm.
6 Determinar el área del cuadrado inscrito en una circunferencia de longitud 18.84 cm.
7 En un cuadrado de 2 m de lado se inscribe un círculo y en este círculo un cuadrado y en este otro círculo. Hallar el área comprendida entre el último cuadrado y el último círculo.
8 El perímetro de un trapecio isósceles es de 110 m, las bases miden 40 y 30 m respectivamente. Calcular los lados no paralelos y el área.
9 A un hexágono regular 4 cm de lado se le inscribe una circunferencia y se le circunscribe otra. Hallar el área de la corona circular así formada.
10 En una circunferencia una cuerda mide 48 cm y dista 7 cm del centro. Calcular el área del círculo.
11 Los catetos de un triángulo inscrito en una circunferencia miden 22.2 cm y 29.6 cm respectivamente. Calcular la longitud de la circunferencia y el área del círculo.
12Sobre un círculo de 4 cm de radio se traza un ángulo central de 60°. Hallar el área del segmento circular comprendido entre la cuerda que une los extremos de los dos radios y su arco correspondiente.
La hipotenusa de un triángulo rectángulo mide 405.6 m y la proyección de un cateto sobre ella 60 m. Calcular:
1 Los catetos.
2 La altura relativa a la hipotenusa.
3 El área del triángulo.









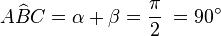
No hay comentarios:
Publicar un comentario