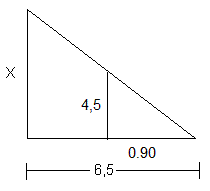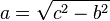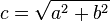*DESCRIBE LA RELACIONES TRIGONOMETRICAS PARA RESOLVER TRIANGULOS RECTANGULOS*
FUNCIONES TRIGONOMETRICAS :
Las
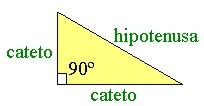
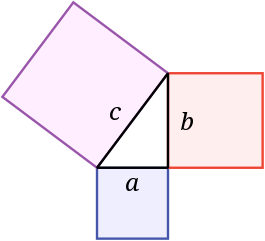
Funciones Trigonométricas, haremos uso del Teorema de Pitágoras y
trabajaremos con las Funciones de Seno, Coseno y Tangente, y sus
inversas.
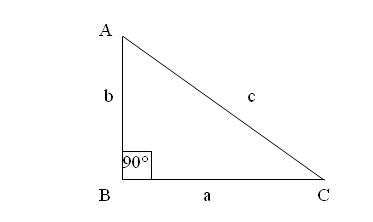
Las letras minúsculas son las que utilizamos en el Teorema de Pitágoras,
las letras Mayúsculas, en éste caso, se utilizarán para referirnos a los
Ángulos del Triángulo.
EL SISTEMA SEXAGESIMAL :
El sistema sexagesimal es un sistema de numeracion posicional que emplea como base aridmetica el número 60 (sesenta). Tuvo su origen en la antigua Babilonia. También fue empleado por los arabes durante el califato omeya. El sistema sexagesimal se usa para medir tiempos (horas, minutos y segundos) y ángulos (grados, minutos y segundos). En dicho sistema, 60 unidades de un orden forman una unidad.
Sistema sexagesimal El Sistema Sexagesimal es un sistema de numeración en el que cada unidad se divide en 60 unidades de orden inferior, es decir, es un sistema de numeración en base 60. Se aplica en la actualidad a la medida del tiempo y a la de la amplitud de los ángulos.
EL SISTEMA CIRCULAR :
En este sistema la unidad de medida es el radián (rad).
Un radián es la medida del ángulo con vértice en el centro de la circunferencia y cuyos lados determinan sobre ella un arco de longitud igual al radio r. Se simboliza 1 rad.

Razones trigonométricas recíprocas
Las razones trigonométricas inversas se definen de la siguiente manera:
- La cosecante (abreviado como csc o cosec), razón recíproca del seno:
- La secante (abreviado como sec), razón recíproca del coseno:
- La cotangente (abreviado como cot), razón recíproca de la tangente:
RESOLUCION DE TRIANGULOS RECTANGULOS :
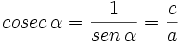
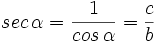
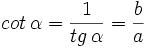


 o
o  .
.